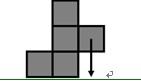
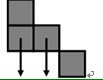
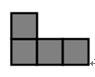
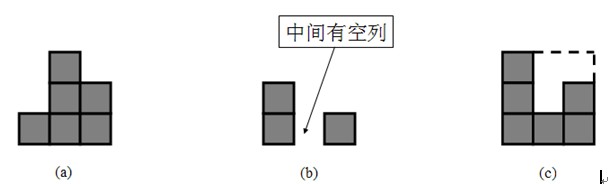
A和B在玩一个射击游戏，战场由若干单位正方形积木组成。积木占据了连续的若干列，且图形周长等于它最小包围矩形的周长。下图(a)是一个合法的战场，但(b)和(c)都不是：(b)中有空列；(c)的图形周长为14，而最小包围矩形（用虚线画出）的周长为12。受重力影响，每个积木的正下方要么是地面，要么是另一个积木。为了让战场看上去错落有致、玩着更刺激，它不能恰好是一个矩形（即：不能每列积木都一样高）。

游戏规则如下：

1、   A和B轮流射击，A先射击。

2、   每次射击时，首先选择一行（该行必须至少有一个积木），以及“左”和“右”中的一个方向，然后往这个方向开火。子弹的威力为1~3的均匀随机整数（即：威力为1、2、3的概率各为1/3），表示子弹能打掉的积木个数，被打掉的积木将直接从战场中消失。如果该行的积木个数小于威力值，则子弹将在打掉该行所有积木后消失。例如，若选择往右射击从下往上数第3行，且威力为2，且这一行一共有4个积木，则最左边的两个积木将被打掉。注意：这两个积木可以不连续。

3、   每次射击完成后，悬空的积木垂直往下落。所有积木不再下落后，下一位选手才能开始射击。

4、   谁打掉了最后一个积木，谁就获胜。

假定开局是，根据规则1，A先开火。射击后，B可能面临的后续局面中的其中三个如下表：

假定A和B都足够聪明，采取让自己获胜概率尽量高的策略，你的任务是计算出A获胜的概率。