在很多 RPG (Role-playing Games) 游戏中,迷宫往往是非常复杂的游戏环节。通常来说,我们在走迷宫的时候都需要花非常多的时间来尝试不同的路径。但如果有了算法和计算机的帮助,我们能不能有更快的方式来解决这个问题?我们可以进行一些尝试。
现在我们有一个 N 行 M 列的迷宫。迷宫的每个格子如果是空地则可以站人,如果是障碍则不行。在一个格子上,我们可以一步移动到它相邻的 8 个空地上,但不能离开地图的边界或者跨过两个障碍的夹缝。下图是一个移动规则的示例。
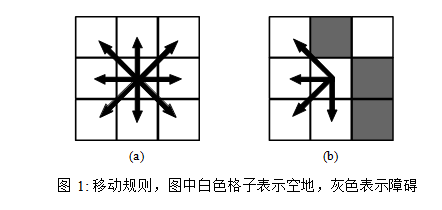
为了离开迷宫,我们还需要触发迷宫中所有的机关。迷宫里总共有 K 个机关,每个机关都落在一个不同的空地上。如果我们到达了某个机关所在的格子时,这个机关就会被自动触发,并在触发之后立即消失。我们的目标是按顺序触发所有的 K 个机关,而当最后一个机关被触发时,我们就可以离开迷宫了。
现在我们已经拿到了迷宫地图,并且知道所有障碍、机关的位置。初始时我们位于迷宫的某个非障碍格子上,请你计算我们最少需要移动多少步才能离开迷宫?
输入的第一行是测试数据的组数 T (T ≤ 20)。
对于每组测试数据:第一行包含地图的行数 N (2 ≤ N ≤ 100),列数 M(2 ≤ M ≤ 100) 和机关的数量 K(1 ≤ K ≤10)。接下来 N 行,每行包含 M 个字符,其中字符 ‘#’ 表示障碍,而 ‘.’ 表示空地。接下来一行描述了我们的初始位置 (x, y),表示我们一开始在第 x 行第 y 列的格子上。这个格子保证是个空地。接下来 K 行,每行给出了一个机关的位置。所有的机关都不会出现在障碍上,并且任意两个机关不会出现在同一个空地上。我们需要按输入给定的顺序触发所有的 K 个机关。
对于每组测试数据,输出离开迷宫所需要的最少步数。如果无论如何都不能离开迷宫,输出 -1。
3
3 3 2
...
...
...
1 1
1 3
2 2
3 3 1
...
.#.
...
1 1
3 3
2 3 1
..#
.#.
1 1
2 3
3
3
-1